|
 |
 |
 |
|||||||
|
|
|
обратная связь | ||||||||
|
Геометрия шахмат и новая теория Нукина Представляем на Ваш суд первую статью нашего нового автора. Сразу скажем - не последнюю! Представляем на Ваш суд первую статью нашего нового автора. Сразу скажем - не последнюю!
С дебютом, Серик!
15 ноября 2008 года исполнилось 60 лет моему тренеру, учителю Нукину Толегену Сатбековичу. Пользуясь сайтом, желаю ему неиссякаемой творческой энергии и сил для поиска шахматной истины. В этот памятный день произошло мое посвящение в тайны новой теории, которое в компании с Александром Юстусом в течение почти двух часов проводил сам юбиляр. Конечно, понять до конца все, что хотел сказать Нукин Т.С., я не смог, поэтому при первой же возможности посмотрел, о чем же пишет большой мастер шахматной игры. Надо заметить, что его новая теория 2NT меня очень заинтересовала. В статьях ставится проблема не просто достижения какого-то минимального перевеса, какого-то хода, пусть даже варианта, в определенной позиции. Названная теория затрагивает глобальную идею нахождения самой сути шахматной игры. Поставить перед собой такую задачу и упорно идти к ее решению может только пытливый и наделенный особым, редким даром ум. "Казыки и керме являются пунктами гармонии фигур. Очень трудный ответ на вопрос "Почему?". Шахматы имеют фланговое развитие, а в этих точках проходят, скрещиваются силовые линии фигур". (Нукин Т.С.). В самом деле, почему? Не расставляя шахматной доски, путем логических и геометрических рассуждений пришел к некоторым умозаключениям относительно особенностей полей с3, с6, f3, f6, с которыми и хотелось бы поделиться. Уважаемый Толеген Сатбекович пишет, что его теория наиболее четко проявляется в эндшпиле. Сразу вспомнился этюд Рети. Ничья. Решение не сложное: 1.Крg7 h4 2.Крf6!! Классика! Заняты поля с6, f6 и белые спасаются в казалось бы безнадежной позиции. 2... h3 3. Кре6 начинается движение к другому магическому полю. 3... h2 4. с7 и т.д. (или 1... Крb6 2. Крf6 - без этого хода никак, 2... h4 3. Кре5 и т.д.) Видимо, в эндшпиле наиболее полно раскрывается сила каждой оставшейся на доске фигуры. Если так, то можно будет немного приблизиться к пониманию секретов магических полей, максимально упростив позицию. Для этого решим очень простые, но интересные задачи. Задача № 1. Белый ферзь на b7. Расположите белого короля таким образом, чтобы количество полей, на которых матовался бы в один ход черный король, было максимальным. Решение: 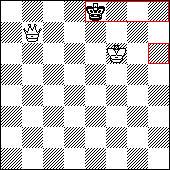
Крf6 (с3). Мат ставится на 5 полях черного короля (h8, g8, f8, e8, h6). Перемещайте белого короля и найдете только 3 поля, где может быть заматован в один ход его визави. Задача № 2. Ферзь там же. Задача та же, только вместо короля необходимо определить поле для белой пешки. При этом пешка не должна двигаться. Решение: 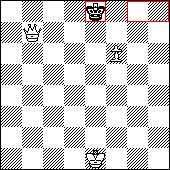
Пешка на f6. Мат ставится на 3 полях черного короля (h8, g8, e8). В других ситуациях - только 2 матующих поля. Ферзя можно переставлять на многие поля, но король и пешка, только находясь на магическом поле, дадут максимальное количество матовых позиций. Задача № 3. Предлагается на выбор а) ферзь; б) ладья и слон; в) ладья и конь. Как видите, номинальная стоимость фигур в этих вариантах примерно одинакова. Выберете тот вариант, при котором возможно заматовать короля. Решение: 
Вариант в). Например, конь на f6, ладья h7, король противника на h8. Конь может стоять только на магическом поле, иначе мата нет. Задача № 4. Составьте максимальное количество матовых позиций со слоном и ферзем, причем слон должен находиться на определенном поле во всех этих позициях, ферзь естественно меняет положение с изменением положения черного короля. Решение: 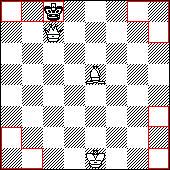
Максимальное количество матовых позиций 12. Слон может располагаться на полях d4, d5, e4, e5. Например, при слоне, расположенном на поле "е5", король матуется на полях a1, a2, а8, b1, b8 (при Фа6), с8, g8, h1, h2, h3, h7, h8. При слоне, находящемся на магических полях, матовых позиций будет 10, а вот стоит снять контроль с магических полей, например при слоне на c4, этих позиций уже будет 8. Вроде задачи только для тех, кто делает первые ходы в шахматах. Но на основе этих задач можно сделать некоторые выводы. 1. Пешка и король, только находясь на магических полях противника, достают угловое поле и в тоже время не утрачивают связь с центром. Это помогло спастись в этюде Рети: через пункт f6 король вылез из углового поля и через е6, е5 успел на противоположный фланг. 2. Конь на магическом поле, приблизившись к угловому полю, сохраняет способность обстреливать максимальное количество полей (8), два из которых являются центральными. Такая способность коня используется в конструкции вечного шаха при ладье на d7. 3. Слон максимально действует на большой диагонали (что, впрочем, и так ясно), но, тем не менее, именно на ней находятся магические поля. В то же время слон на магическом поле теряет свою дальнобойность, вернее, количество простреливаемых полей. 4. Интересно, что ферзь, только находясь на магическом поле, в то же время простреливает остальные магические поля. Ладья на магическом поле простреливает два других. Выводов много, но нет чего-то главного. Рассуждаем дальше. В данных примерах можно заметить, что с магического поля помимо контроля над флангом (вплоть до углового поля) не снимается контроль над центром. Чтож, вернемся к центру. Ставьте на центральные поля d4, d5, e4, e5 последовательно ферзя (который включает в себя ходы всех фигур, кроме коня) и коня (хотя конь требуется только для чистоты эксперимента). Отмечайте те поля, которые они достают. Результат: остались не обстрелянными 8 полей (а3, а6, с1, с8, f1, f8, h3, h6). Интересно, что будет на магических полях. Задача № 5. Последовательно ставя ферзя и коня, найдите поле, на котором были бы обстреляны этими фигурами все поля центра (d4, d5, e4, e5) и королевского фланга черных. Решение: 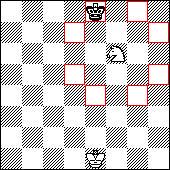
Поле f6. Конь с f6 обстреливает поля d5, d7, e4, e8, g4, g8, h5, h7, ферзь с этого поля добьет оставшиеся. Другого поля нет. Смещаясь в какую-либо сторону от этого поля, Вы потеряете либо какое-то поле в центре, либо на фланге. Только с f6 Вы обстреливаете королевский фланг противника, не потеряв контроля ни над одним центральным полем. Таким образом, владея своим магическим полем, Вы имеете возможность максимально контролировать центр и защитить любое поле своего фланга. Владея магическим полем противника, Вы получаете возможность атаковать все поля фланга противника, сохраняя контроль за всеми центральными полями. Посмотрите на геометрию. Выделите поля в квадрате d4, d8, h4, h8 (то есть включите все центральные и угловые поля королевского фланга черных). Центр этого квадрата - поле f6! Шахматы имеют не просто фланговое, а центрально-фланговое развитие. Шахматные фигуры движутся с флангов к центру, с центра возвращаются на фланг, концентрируются на каком-то фланге через центр и т.д. А главными (но, конечно, не единственными) точками пересечения между центром и флангом являются магические поля. Убежден, что именно в контексте борьбы за центр, контроля над центром, эффективного использования центра надо рассматривать владение магическими полями. "Если в малом повторяется большое, если из одной клетки вырастили овцу Долли, то можно предположить, что и вся солнечная система - квадрат, вся галактика - квадрат, и всё это квадрат в квадрате! И законы углов квадрата как болевые точки присущи всему!". А эти слова Нукина Т.С. просто за гранью понимания! Но! Ведь 4 или два в квадрате или четыре в первой степени - это центр. 4 в квадрате (или квадрат в квадрате!!!) есть 16 - а это магический квадрат, 4 в кубе (Вот так! Есть еще квадрат в кубе!!! К этому кубу мы еще вернемся) - это 64, то есть вся шахматная доска. Получается, что магический квадрат - производная от центра, а шахматная доска - производная от магического квадрата. А как Вам такая задача? Задача № 6. На шахматной доске найдите три квадрата. Причем, угловое поле первого квадрата, является угловым полем второго квадрата, а угловое поле второго квадрата является центром третьего квадрата. Но это не всё. Сумма площадей двух квадратов равняется площади третьего квадрата.
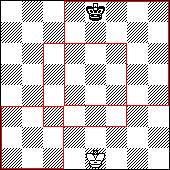
Первый квадрат с угловыми полями а1, а3, с1, с3. Второй квадрат - с3, с6, f3, f6. Третий квадрат - d4, d8, h4, h8 (центр f6). Площади квадратов 9, 16, 25 (9+16=25). Сторона квадрата планомерно увеличивается - 3, 4, 5. Возможно, что эта задача интерпретируется следующим образом. Первый квадрат - это дебют. Белые и черные укрепляют свои магические поля. Кстати, заметьте, что уже в первоначальной расстановке магические поля являются наиболее укрепленными (атакуются 2 пешками и конем). Второй квадрат - это миттельшпиль. Борьба разворачивается в магическом квадрате за магические поля противника. Третий квадрат - эндшпиль. Апофеоз. Магическое поле не просто угловое поле, а центральное. Еще раз обращу внимание, что помимо угловых полей всего фланга противника в этот квадрат вошли все центральные поля. "Когда захватываешь это поле, то возникает паралич всей позиции противника, в то время как собственные фигуры максимально активизируются". Лучше Толегена Сатбековича не скажешь. Это, что касается полей с3, с6, f3, f6. Определенная логика в этих полях есть. Тогда откуда взялся прямоугольник с4-с5-f4-f5 на квадратной доске? "Слова "казык" и "керме" я придумал не сам, а просто взял их из шашек" - пишет учитель. Из шашек... Поговорим немного о шашках. Что же такое кол (казык) в русских шашках? Кол: 1. Белая (черная) простая c5 (f4), сдерживающая шашки a5 и a7 или a5 и e7 (h2 и h4 или d2 и h4); 2. Начало в русских шашках, с основными ходами 1.cd4 ba5 2.dc5 d:b4 3.a:c5. В самом деле, те, кто хотя бы немного знаком с позиционной теорией шашечной игры, знают, что шашисты очень большое значение придают пунктам c5 и f4. Задача № 7. Тогда следующий вопрос. Почему же появляется такой прямоугольный центр на квадратной шашечной доске? Ответ: В шашках уже в первоначальной позиции левый фланг сильнее правого, поэтому (по принципу играй там, где ты сильнее) шашисты борются за захват пунктов с5 (f4) и предпочитают играть левым флангом. Но это теория, а как такое геометрическое объяснение? Борьба в шашках ведется на 32 полях черного цвета. А из 32-х квадрата не получить, возможен только прямоугольник 8х4. Значит можно предположить, что и гармония шашек должна быть прямоугольной, вытянутой. Соответственно и центр возможен прямоугольный с4-с5-f4-f5, но из них только 4 поля "рабочих", черных. Может поэтому, в поисках истинного квадрата, шашечная доска имеет различные модификации (ищет стабильности по Нукину Т.С.): есть 100 клеточные шашки и даже 144 клеточные. На эту тему пусть думают шашисты, но я уверен точно: что приемлемо в шашках, не может подойти в шахматах. Наш центр - квадратный. Доказательство от противного. Все гениальное - просто! Просто как стул. В самом деле, обведите поля d4, d5, e4, e5, с3, с6, f3, f6. Что получилось? 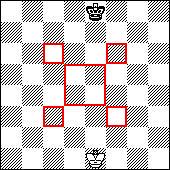
Стул. Поля с3, с6, f3, f6 - это ножки или опоры центра. Подрежьте, к примеру, опору f6 и стул начнет заваливаться на королевский фланг черных. Р.S. Подобно Толегену Сатбековичу дадим волю своему воображению и немного пофантазируем. Попробуйте связать шахматы и египетские пирамиды. Мне это сумасшедшим образом удалось. Для этого вернемся к "четыре в кубе". Раз появился куб, значит должна быть объемная фигура. Посмотрим на шахматную доску сверху, прочертим диагонали. Какую фигуру напоминает? 
Пирамиду. Возможно шахматная доска - это пирамида, разложенная на плоскости. Человеческому мозгу проще оперировать в плоскости. Как карта, вывешенная на доске, отображает земной шар. Теперь о чатуранге, прародительнице шахмат. Почему в чатурангу играли вчетвером? Ведь, если чатуранга - калька расстановки военных армий, то играли бы вдвоем. Участвует в войне только две армии, четыре - только частный случай. Возможно, что чатуранга появилась как военная модификация какой-то промежуточной игры, которая в свою очередь связана с картами возведения египетских пирамид. Пирамиду строили с четырех сторон, отсюда и идут четыре нелогичные армии в чатуранге. Известно, что для строительства пирамиды создавались команды, имелось что-то похожее на соцсоревнование, во главе команды ставились прорабы, т.е. имелась иерархия. Можно предположить, что имелась карта каждой стороны пирамиды, по которой контролировалось ее строительство. Она делилась на ячейки, соответственно тем каменным глыбам (или блокам глыб), которые укладывались в пирамиду, прообразы шахматных квадратов. Опять таки именно наличие квадратов, некая дискретность доски, не характерны для военных действий (тяжело представляется, чтобы карта древних военачальников была поделена на мелкие квадраты). Постепенно, пока пирамида строилась, строители пирамиды ползли вверх, как пешки (только вверх) и они постоянно подгонялись прорабами, или еще какими-то начальниками (т.е. на карте они тоже имели соответствующие обозначения, но отличные от строителей, как фигуры отличаются от пешек и между собой). Чатуранга взяла еще одно свойство от возведения пирамиды - это медлительность, что не характерно для военных действий. Фигуры в чатуранге перемещались очень медленно. Постепенно чатуранга начала совершенствоваться. Избавились от двух ненужных армий, сделали две, фигуры стали мобильней. Так появился шатрандж. После дальнейших изменений в правилах игры появились шахматы. "Gens una Sumus". Дата: 26.11.08 08:29 Автор: Серик Солтанов, мастер ФИДЕ |
|